Ebben a modellben az ujjak számának, típusának kialakulását fogjuk vizsgálni. A szám és a típus a végtagbimbó növekedésének korai stádiumában alakul ki. Azt, hogy egy ujj milyen lesz, a végtagbimbó egyik szélén kibocsátott morfogén anyag határozza meg. Ennek különböző (abszolút vagy relatív) nagyságától függ, hogy melyik ujjkezdeményből milyen ujj lesz.
Vegyük a sejtautomata elvű diffúziós modellt. A sejttáblázat egy sorát (1. sor) feleltessük meg a végtagbimbó aktív részének (ami itt történik, az befolyásolja az ujjak kialakulását). A modell szimulációs lépését egy kicsit pontosítsuk.
Szimulációs lépés:
U:=R
Ciklus i=1-től N-ig
Ciklus j=1-től M-ig
Ha U(i,j)≠0 akkor Változás(i,j)
Ciklus vége
Ciklus vége
Állapot meghatározás
Eljárás vége.
Az ujjak kialakulását a Volpert-től származó "Francia zászló" modellel szemléltetjük. Ebben 3 különböző típusú sejt fog kialakulni: P (piros), F (fehér) és K (kék).
1. variáció: A három színt abszolút koncentrációk alakítják ki, ha a koncentráció értéke nagyobb egy H1 értéknél, akkor a sejt P állapotba kerül, ha H1 és H2 közötti, akkor F állapotba, s ha H2-nél kisebb, akkor K állapotba.
Állapot meghatározás:
Ciklus j=1-től N-ig
Elágazás
U(1,j)≥H1 esetén A(j):="P"
U(1,j)<H1 és U(1,j)≥H2 esetén A(j):="F"
U(1,j)<H2 esetén A(j):="K"
Elágazás vége
Ciklus vége
Eljárás vége.
A modell vizsgálatakor nagyon hamar felmerülnek problémák, amelyek használatát lehetetlenné teszik. A diffúzió hatása ugyanis az, hogy egy idő után a morfogén anyag egyenletesen oszlik el a vizsgált térrészben, s így egyforma ujjakat, egyszínű zászlót kapunk. A másik probléma, hogy a kísérleti megfigyelések azt mutatják, hogy a morfogén anyag mennyiségének megkettőzése, felezése nem befolyásolja sem az ujjak számát, sem pedig milyenségét.
2. variáció: A három színt relatív koncentrációk alakítják ki, ha a sejt és szomszédjai közötti koncentrációkülönbség értéke nagyobb egy H1 értéknél, akkor a sejt P állapotba kerül, ha H1 és H2 közötti, akkor F állapotba, s ha H2-nél kisebb, akkor K állapotba.
Állapot meghatározás:
Ciklus j=1-től N-ig
A:=|U(1,j-1)-U(1,j)| + |U(1,j+1)-U(1,j)|
Elágazás
A≥H1 esetén A(j):="P"
A<H1 és A≥H2 esetén A(j):="F"
A<H2 esetén A(j):="K"
Elágazás vége
Ciklus vége
Eljárás vége.
Ez a modell is hibásan működik akkor, amikor a morfogén anyag egyenletesen eloszlik a vizsgált térrészben. Ezen probléma megoldására két út áll előttünk.
1. lehetőség: A vizsgálatokat csak bizonyos időtartamig végezhetjük (amíg az ujjakat meghatározó sejtek a végtagbimbó aktív zónájában vannak). Ha ez az idő kisebb, mint a kiegyenlítődés ideje, akkor a modellben a különbözőség rögzítődik.
2. lehetőség: Adjuk meg a sejt három állapotának sorrendjét (szintjét), a nagyobb koncentrációjúak legyenek magasabb szintűek. Rögzítsük azt a szabályt, hogy magasabb szintről visszalépni már nem lehet. Így szintén megkaphatjuk a kívánt különbözőséget.
Állapot meghatározás:
Ciklus j=1-től N-ig
A:=|U(1,j-1)-U(1,j)| + |U(1,j+1)-U(1,j)|
Elágazás
A≥H1 esetén A(j):="P"
A<H1 és A≥H2 és A(j)≠"P" esetén A(j):="F"
A<H2 és A(j)≠"P" és A(j)≠"F" esetén A(j):="K"
Elágazás vége
Ciklus vége
Eljárás vége.
A foltképződési modellek általában kémiai körfolyamatokra vezethetők vissza. A biokémiai folyamatokban még azonos fajok esetén is különböző mintázatok jöhetnek létre.
1.: egy vörösesbarna foltos afrikai zsiráf. 2.: két sötétbarna foltos afrikai zsiráf. 3. és 4.: számítógépes szimuláció eredménye nagy, ill. kisebb méretű fekete foltok fehér alapon.A foltok általában több körfolyamat egymásra hatása miatt alakulnak ki.
Az első modellben vegyünk két önreprodukáló kémiai körfolyamatot, amelyek egymás termékeit fogyasztják!
X + A1 → A2 | Y + B1 → B2 |
A2 → Y + A3 | B2 → X + B3 |
A3 → A1 + A1 | B3 → B1 + B1 |
Összegképletük:
X + A → Y + A + A | Y + B → X + B + B |
A reakciókinetikai modellt általánosítsuk úgy, hogy a körfolyamat alkotóelemeit külön-külön nem ábrázoljuk, valamint ezeket molekula helyett azonnal festékanyagot tartalmazó, illetve azt nélkülöző sejteknek tekintjük!
Az X és az Y molekulák mozoghassanak, az A és a B pedig legyenek különböző festékanyagokat tartalmazó sejtek, amelyek természetesen mozdulatlanok! A feladat egyszerű megoldása miatt érdemes a vizsgált teret két példányban tárolni, az egyikben csak a sejtek lesznek, a másikban pedig a molekulák.
A foltos felület növekedésével ne foglalkozzunk! Ezt úgy lehet például kiküszöbölni, hogy a sejtek táblázatában felveszünk üres helyeket, amelyek irányába a foltok növekedhetnek.
A molekulákat tároljuk a MOL(N,M) mátrixban, a sejteket pedig az SEJT(N,M)-ben. Az A és a B sejtek elpusztulhatnak, a pusztulásuk valószínűségét jelölje P, illetve Q!
Szimulációs lépés:
(I,J):=véletlen hely(N,M)
(K,L):=véletlen szomszéd(I,J)
Csere(MOL(I,J),MOL(K,L))
Elágazás
SEJT(I,J)="A" és véletlenszám<P esetén SEJT(I,J):=" "
SEJT(I,J)="B" és véletlenszám<Q esetén SEJT(I,J):=" "
Elágazás vége
Elágazás
MOL(I,J)="X" és SEJT(I,J)="A" esetén Keletkezés(I,J,"A","Y")
MOL(I,J)="Y" és SEJT(I,J)="B" esetén Keletkezés(I,J,"B","X")
Elágazás vége
Eljárás vége.
Keletkezés(I,J,SE,MO):
MOL(I,J):=MO
véletlen üres szomszéd keresés(I,J,K,L)
SEJT(K,L):=SE
Eljárás vége.
A kapott eredmény, bár dinamikusan változik, de a következőhöz lesz hasonló:
Kis foltok szimulációjaÁltalánosítsunk tovább: a reakciókban résztvevő molekulákkal ne foglalkozzunk, hatásukat a sejtek szomszédszáma alapján vegyük figyelembe!
Ebben a modellben minden sejt alakuljon olyanná, amilyen szomszédjából több van! A sejttáblázat legyen mindig tele A- és B-típusú sejtekkel!
Szimulációs lépés:
(I,J):=véletlen hely(N,M)
Szomszédszámolás(I,J,"A",A)
Szomszédszámolás(I,J,"B",B)
Elágazás
SEJT(I,J)="B" és A >B esetén SEJT(I,J):="A"
SEJT(I,J)="A" és A<B esetén SEJT(I,J):="B"
Elágazás vége
Eljárás vége.
Érdekes módon függ a foltosodás a vizsgált tér méretétől is. Ha a szimulációs terünk kicsi a szomszédszámolás távolságához képest, akkor az eredmény egy egyszínű tér lesz, vagy esetleg egy-két folt látható:
KecskegidaHa a tér mérete nagy, akkor több nagyméretű folt fog keletkezni, véletlenszerű eloszlásban:
A foltok mérete és alakja függ K szomszédszám nagyságától. Ha a szomszédszámot nagyobb távolságra számoljuk, a foltok határvonala simább lesz.
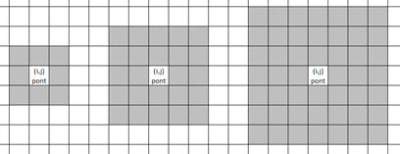Minta K=1, 2 illetve 3 szomszédszámraHa a szomszédszámok között 1-nél nagyobb különbséget várunk el, akkor görbébb lehet a határ.
Szimulációs lépés:
(I,J):=véletlen hely(N,M)
Szomszédszámolás(I,J,"A",A)
Szomszédszámolás(I,J,"B",B)
Elágazás
SEJT(I,J)="B" és A >B-DB esetén SEJT(I,J):="A"
SEJT(I,J)="A" és A-DB<B esetén SEJT(I,J):="B"
Elágazás vége
Eljárás vége.
Rövid idővel a szimuláció indítás után...
A szimulációs program indításakor
... és egy stabilizálódott minta K=4 esetén.Ha a tér egy csíkhoz hasonlít (azaz pl. oszlopszáma lényegesen nagyobb, mint a sorainak száma), akkor csíkos mintázat alakul ki:
ZebrákEz utóbbi különösen akkor lesz látványos, ha a csíkot egy kiterített hengerfelületnek fogjuk fel (így a hosszabb oldalak melletti pontok szomszédosak lesznek a szemben levő oldal melletti pontokkal).
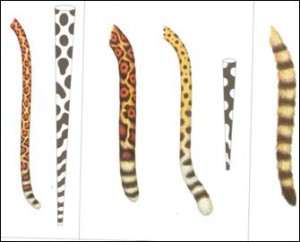Állatok farka és hengeres modelljeikA tér formáját jobban megváltoztatva egészen érdekes mintázatokat is kaphatunk:
 Zebra irhája |  és modellje |
Módosítsuk az előző modellt úgy, hogy ne engedjük meg olyan sejtek kialakulását, amelyeket csak velük azonos típusú sejt vesz körül.
Szimulációs lépés:
(I,J):=véletlen_hely(N,M)
Szomszédszámolás(I,J,"A",A)
Szomszédszámolás(I,J,"B",B)
Elágazás
SEJT(I,J)="B" és A >B esetén SEJT(I,J):="A"
SEJT(I,J)="A" és A<B esetén SEJT(I,J):="B"
Elágazás vége
Ha SEJT(I,J)="A" és B=0 akkor SEJT(I,J):="B"
Ha SEJT(I,J)="B" és A=0 akkor SEJT(I,J):="A"
Eljárás vége.
Ha nagyobb pöttyöket akarunk megengedni, akkor az A=0, B=0 feltételeket kell kicserélnünk a pötty lehetséges mérethatárára (MH).
Szimulációs lépés:
(I,J):=véletlen_hely(N,M)
Szomszédszámolás(I,J,"A",A)
Szomszédszámolás(I,J,"B",B)
Elágazás
SEJT(I,J)="B" és A >B esetén SEJT(I,J):="A"
SEJT(I,J)="A" és A<B esetén SEJT(I,J):="B"
Elágazás vége
Ha SEJT(I,J)="A" és B<MH akkor SEJT(I,J):="B"
Ha SEJT(I,J)="B" és A<MH akkor SEJT(I,J):="A"
Eljárás vége.
 Nagy foltos mintázat pöttyökkel |  Leopárd |
Szabálytalan (kanyargó) csíkok alakulnak ki, ha a két sejtre különböző szabályok érvényesek. Egy A-típusú sejt alakuljon át B-vé, ha van B-szomszédja, a B-típusú pedig A-vá, ha az A-szomszédjai száma kisebb, mint a B-szomszédjai száma!
Szimulációs lépés:
(I,J):=véletlen_hely(N,M)
Szomszédszámolás(I,J,"A",A)
Szomszédszámolás(I,J,"B",B)
Elágazás
SEJT(I,J)="A" és B >0 esetén SEJT(I,J):="B"
SEJT(I,J)="B" és A<B esetén SEJT(I,J):="A"
Elágazás vége
Eljárás vége.
A csíkok vastagsága, egyenletessége itt is a szomszédság méretétől függ. (A B>0, A<B feltételeket itt is módosíthatjuk.)
Szabálytalan csíkok
 |
 |
 |
| Készült az "Országos koordinációval a pedagógusképzés megújításáért” című TÁMOP-4.1.2.B.2-13/1-2013-0007 pályázat keretében. (ISBN 978-963-284-631-6) | ||
A tananyag az ELTESCORM keretrendszerrel készült