Szimulációs modellek a biológiában

2. Populációdinamika

Először elemi populációnövekedéssel foglalkozunk. Ezt tulajdonképpen már vizsgáltuk a szimuláció alapjairól szóló leckében (Modellezés és szimuláció) elemi növekedési modellek címen. Most ugyanezt nézzük meg más szempontból, s kicsit részletesebben.

2.1. Exponenciális növekedés

A legegyszerűbb esetben az egyedenkénti szaporodási, illetve halálozási ráták semmitől sem függnek, a vizsgált időszakban állandóak, a létszám az újszülöttekkel nő, a meghaltakkal pedig csökken. A létszámváltozást leíró egyenlet:

ahol b az egy egyedre egy időegység alatt eső utódok átlagos száma, d pedig a halálozásuk valószínűsége.

A modellhez tároljuk az aktuálisan létező egyedek számát az N változóban (az egyedek egyenkénti megadására egyelőre nincs szükség)! Minden egyed d valószínűséggel hal meg, és b paraméterű, Poisson eloszlású véletlenszám adja meg utódai számát. Alkalmazzuk a generációs keretmodellt!

Akár a fenti differenciálegyenletet oldjuk meg, akár a szimulációs programot használjuk, eredményként azt kapjuk, hogy a populáció mérete exponenciálisan nő vagy csökken. (A szimulációs programnál természetesen vannak véletlen ingadozások, ezért rá ez az állítás csak statisztikus értelemben lesz igaz.)

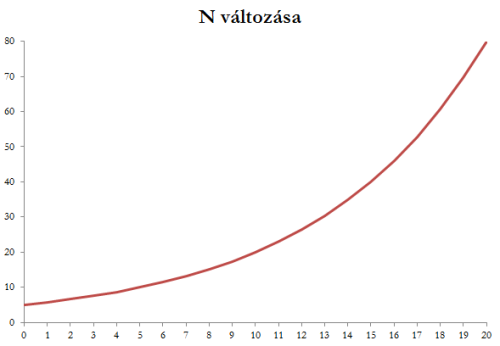Exponenciális növekedés - matematikai módszerrel kapott görbe részlete.

Ez a növekedés azonban a természetben csak nagyon szűk körülmények között tartható fenn, amikor a populáció még messze van az élettere teljes kitöltésétől. Ez azonban valós körülmények között legtöbbször nem igaz, a születési és a halálozási ráták függnek az egyedszámtól.

Vissza a tartalomjegyzékhez

2.2. Logisztikus növekedés

Módosítsuk az előző modell paramétereit, tegyük létszámfüggővé őket:

A születési és a halálozási ráta is tartalmaz egy a létszámtól függő lineáris tényezőt. (A gyakorlatban legtöbbször a K_b >0 és a K_d >0.) Ekkor a szimulációs lépés így néz ki:

Ebben az esetben a populáció nem növekszik tovább, ha a létszám elér egy határértéket. A növekedés módosított egyenletéből ez a határ kiszámítható:

Az r = b₀ – d₀ jelölést bevezetve a logisztikus növekedés egyenlete átírható a tankönyvek által általában közölt formába:

A modell kétféle eredményt adhat: a populáció létszáma az egyensúlyi állapot felé haladva növekszik vagy csökken.

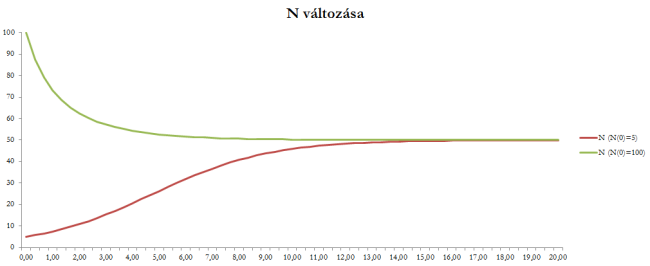Logisztikus növekedés - matematikai módszerrel kapott két görbe részlete. A piros görbe tartozik az N(0)=5 kezdőértékhez, a zöld az N(0)=100-hoz.

A matematikai modellel ellentétben, a szimulációs modellben könnyű megvalósítani a létszámtól való másféle függést is, csupán a szimulációs lépés elején szereplő két képletet kell átírni.

Ebben a modellben az egyensúlyi állapotot – statisztikusan – monoton függvénnyel érjük el, a létszámgörbe egyik irányból sem lépi túl az egyensúlyi állapotot. Ha azonban a létszámváltozást nem az aktuális időpillanatbeli létszámtól, hanem egy múltbeli ( Δt -vel korábbi) állapottól tesszük függővé, akkor túllengés is bekövetkezhet.

Ekkor háromféle eredmény fordulhat elő:

1. az ingadozás csillapodik,

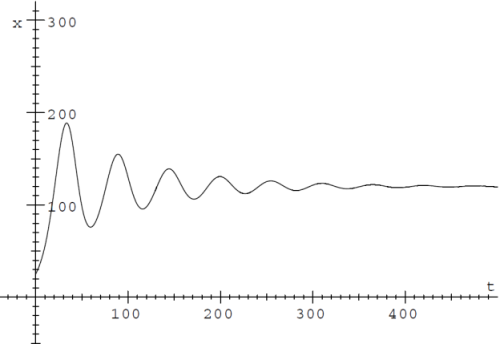Logisztikus növekedés - matematikai módszerrel kapott görbe részlete. Csillapodó eset. (r=0.1, K=120, Δt=13)

2. az ingadozás növekszik, s így a populáció előbb-utóbb kihal,

3. illetve a létszám periodikusan változik.

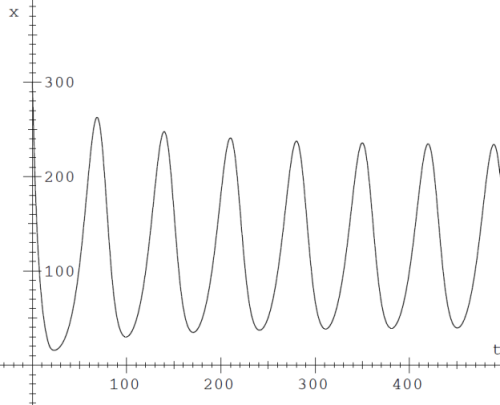Logisztikus növekedés - matematikai módszerrel kapott görbe részlete. Lényegében periodikus eset. (r=0.1, K=120, Δt=17)

Egy populációra persze általában nem egyetlen létszámfüggő erő hat, hanem több, ezért K_b és K_d is több tényezőből számítandó, például ezek összegeként, vagy esetleg súlyozott összegeként; az alábbi formula a legegyszerűbb esetet írja le:

Ez a szimulációs modellen lényegében nem változtat, csupán a modell paraméterei számát növeli meg. A módosított algoritmusban B(NB) , illetve D(ND) jelöli a létszámfüggő hatóerők nagyságát. A szimulációs lépés előtt kiszámítandó KB , illetve KD értéke:

Vissza a tartalomjegyzékhez

2.3. Két nem vizsgálata

Próbáljunk egy másfajta módosítást, különböztessük meg egymástól a két nemet!

Ekkor természetesen kétféle halálozási rátára van szükség (D1, D2) , születési ráta viszont csak az egyik nemhez tartozik. Itt viszont meg kell adni, hogy az utódok hányadrésze tartozik az egyik, illetve a másik nemhez – ezzel egyenértékű, ha a kétféle nemű utódokhoz két születési rátát adunk meg (B1,B2) . Legyen N1 és N2 a két nem létszáma!

Könnyű észrevenni, hogy N2=0 , B2=0 esetén a modell ugyanazt az eredményt adja, mintha e fejezet legelső modelljében N=N1 , B=B1 , D=D1 paramétereket választottuk volna, azaz ahhoz képest nem kapunk lényegében különböző eredményeket.

Az már más kérdés, hogy a két nem különböző egyedszáma milyen társas kapcsolatok beli különbözőségeket okozhat a populációban.

Vissza a tartalomjegyzékhez